Abstract
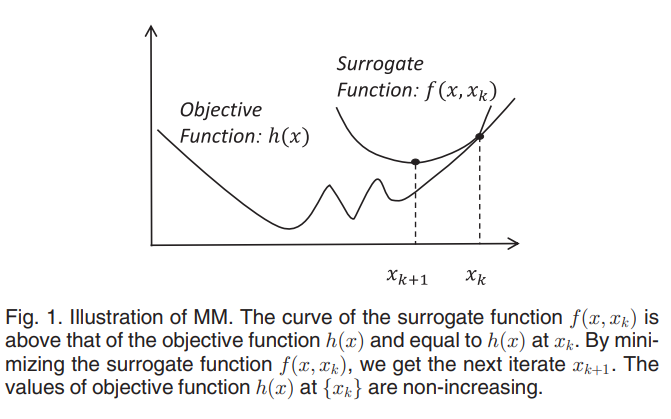
L1 -norm based low rank matrix factorization in the presence of missing data and outliers remains a hot topic in computer vision. Due to non-convexity and non-smoothness, all the existing methods either lack scalability or robustness, or have no theoretical guarantee on convergence. In this paper, we apply the Majorization Minimization technique to solve this problem. At each iteration, we upper bound the original function with a strongly convex surrogate. By minimizing the surrogate and updating the iterates accordingly, the objective function has sufficient decrease, which is stronger than just being non-increasing that other methods could offer. As a consequence, without extra assumptions, we prove that any limit point of the iterates is a stationary point of the objective function. In comparison, other methods either do not have such a convergence guarantee or require extra critical assumptions. Extensive experiments on both synthetic and real data sets testify to the effectiveness of our algorithm. The speed of our method is also highly competitive.