Relaxed Majorization-Minimization for Non-smooth and Non-convex Optimization

Abstract

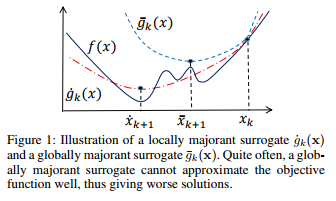
We propose a new majorization-minimization (MM) method for non-smooth and non-convex programs, which is general enough to include the existing MM methods. Besides the local majorization condition, we only require that the difference between the directional derivatives of the objective function and its surrogate function vanishes when the number of iterations approaches infinity, which is a very weak condition. So our method can use a surrogate function that directly approximates the non-smooth objective function. In comparison, all the existing MM methods construct the surrogate function by approximating the smooth component of the objective function. We apply our relaxed MM methods to the robust matrix factorization (RMF) problem with different regularizations, where our locally majorant algorithm shows great advantages over the state-of-the-art approaches for RMF. This is the first algorithm for RMF ensuring, without extra assumptions, that any limit point of the iterates is a stationary point.