t-Schatten- p Norm for Low-Rank Tensor Recovery

Abstract

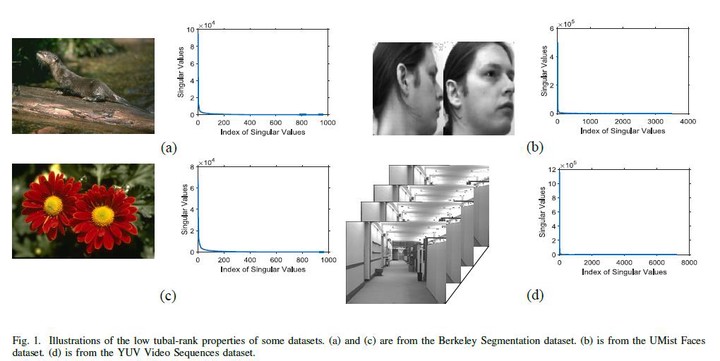
In this paper, we propose a new definition of tensor Schatten-p norm (t-Schatten-p norm) based on t-SVD, and prove that this norm has similar properties to matrix Schatten-p norm. More importantly, the t-Schatten-p norm can better approximate the l1 norm of the tensor multi-rank with 0 < p < 1. Therefore it can be used for the Low-Rank Tensor Recovery problems as a tighter regularizer. We further prove the tensor multi-Schatten-p norm surrogate theorem and give an efficient algorithm accordingly. By decomposing the target tensor into many small-scale tensors, the non-convex optimization problem (0 < p < 1) is transformed into many convex sub-problems equivalently, which can greatly improve the computational efficiency when dealing with large-scale tensors. Finally, we provide the theories on the conditions for exact recovery in the noiseless case and give the corresponding error bounds for the noise case. Experimental results on both synthetic and real-world datasets demonstrate the superiority of our tSchattern-p norm in the Tensor Robust Principle Component Analysis (TRPCA) and the Tensor Completion (TC) problems.