Tensor Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Tensors via Convex Optimization

Abstract

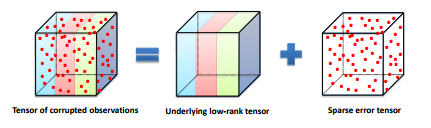
This paper studies the Tensor Robust Principal Component (TRPCA) problem which extends the known Robust PCA to the tensor case. Our model is based on a new tensor Singular Value Decomposition (t-SVD) and its induced tensor tubal rank and tensor nuclear norm. Consider that we have a 3-way tensor X \in R^{n1×n2×n3} such that X = L_0 + S_0, where L0 has low tubal rank and S_0 is sparse. Is that possible to recover both components? In this work, we prove that under certain suitable assumptions, we can recover both the low-rank and the sparse components exactly by simply solving a convex program whose objective is a weighted combination of the tensor nuclear norm and the 1-norm. Interestingly, TRPCA involves RPCA as a special case when n3 = 1 and thus it is a simple and elegant tensor extension of RPCA. Also numerical experiments verify our theory and the application for the image denoising demonstrates the effectiveness of our method.