Optimized Projections for Compressed Sensing via Direct Mutual Coherence Minimization

Abstract

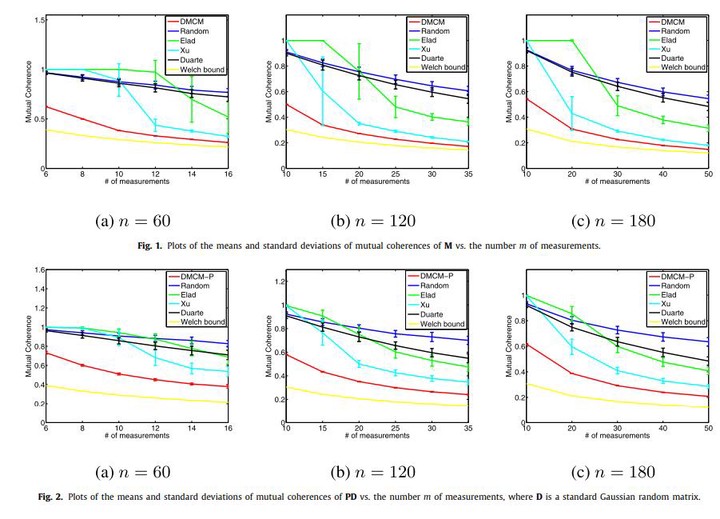
Compressed Sensing (CS) is a new data acquisition theory based on the existence of a sparse representation of a signal and a projected dictionary PD, where P ∈ R^(m×d) is the projection matrix and D ∈ R^(d×n) is the dictionary. To recover the signal from a small number m of measurements, it is expected that the projected dictionary PD is of low mutual coherence. Several previous methods attempt to find the projection P such that the mutual coherence of PD is low. However, they do not minimize the mutual coherence directly and thus they may be far from optimal. Their used solvers lack convergence guarantee and thus the quality of their solutions is not guaranteed. This work aims to address these issues. We propose to find an optimal projection matrix by minimizing the mutual coherence of PD directly. This leads to a nonconvex nonsmooth minimization problem. We approximate it by smoothing, solve it by alternating minimization and prove the convergence of our algorithm. To the best of our knowledge, this is the first work which directly minimizes the mutual coherence of the projected dictionary and has convergence guarantee. Numerical experiments demonstrate that our method can recover sparse signals better than existing ones.