Abstract
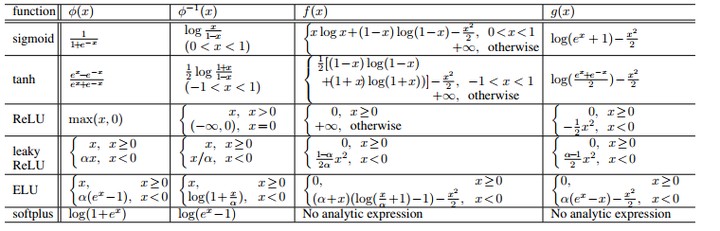
We propose a new optimization method for training feed-forward neural networks. By rewriting the activation function as an equivalent proximal operator, we approximate a feed-forward neural network by adding the proximal operators to the objective function as penalties, hence we call the lifted proximal operator machine (LPOM). LPOM is block multi-convex in all layer-wise weights and activations. This allows us to use block coordinate descent to update the layer-wise weights and activations. Most notably, we only use the mapping of the activation function itself, rather than its derivative, thus avoiding the gradient vanishing or blow-up issues in gradient based training methods. So our method is applicable to various non-decreasing Lipschitz continuous activation functions, which can be saturating and non-differentiable. LPOM does not require more auxiliary variables than the layer-wise activations, thus using roughly the same amount of memory as stochastic gradient descent (SGD) does. Its parameter tuning is also much simpler. We further prove the convergence of updating the layer-wise weights and activations and point out that the optimization could be made parallel by asynchronous update. Experiments on MNIST and CIFAR-10 datasets testify to the advantages of LPOM.