Classification via Minimum Incremental Coding Length (MICL)

Abstract

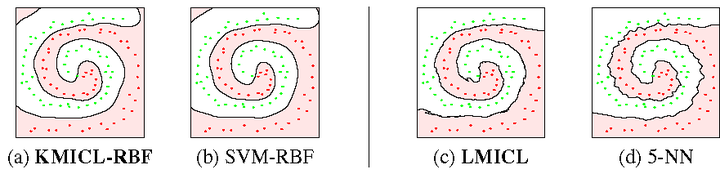
We present a simple new criterion for classification, based on principles from lossy data compression. The criterion assigns a test sample to the class that uses the minimum number of additional bits to code the test sample, subject to an allowable distortion. We rigorously prove asymptotic optimality of this criterion for Gaussian data and analyze its relationships to classical classifiers. The theoretical results provide new insights into the relationships among a variety of popular classifiers such as MAP, RDA, k-NN, and SVM. Our formulation induces several good effects on the resulting classifier. First, minimizing the lossy coding length induces a regularization effect which stabilizes the (implicit) density estimate in a small sample setting. Second, compression provides a uniform means of handling classes of varying dimension. The new criterion and its kernel and local versions perform competitively on synthetic examples, as well as on real imagery data such as handwritten digits and face images. On these problems, the performance of our simple classifier approaches the best reported results, without using domain-specific information. All MATLAB code and classification results will be made publicly available for peer evaluation.