Contextual Distance for Data Perception

Abstract

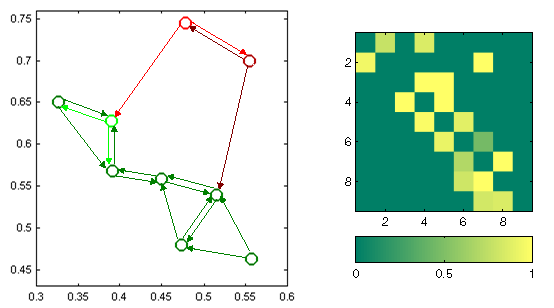
Structural perception of data plays a fundamental role in pattern analysis and machine learning. In this paper, we develop a new structural perception of data based on local contexts. We first identify the contextual set of a point by finding its nearest neighbors. Then the contextual distance between the point and one of its neighbors is defined by the difference between their contribution to the integrity of the geometric structure of the contextual set, which is depicted by a structural descriptor. The centroid and the coding length are introduced as the examples of descriptors of the contextual set. Furthermore, a directed graph (digraph) is built to model the asymmetry of perception. The edges of the digraph are weighted based on the contextual distances. Thus direction is brought to the undirected data. And the structural perception of data can be performed by mining the properties of the digraph. We also present the method for deriving the global digraph Laplacian from the alignment of the local digraph Laplacians. Experimental results on clustering and ranking of toy problems and real data show the superiority of asymmetric perception.