Tensor LRR Based Subspace Clustering

Abstract

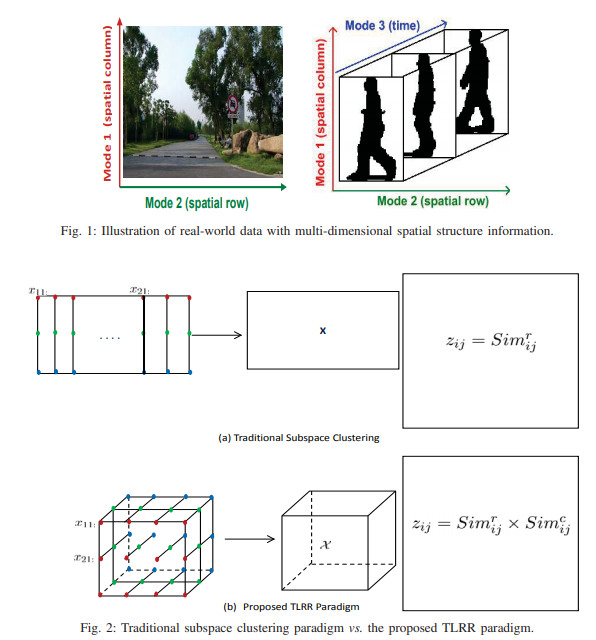
Subspace clustering groups a set of samples (vectors) into clusters by approximating this set with a mixture of several linear subspaces, so that the samples in the same cluster are drawn from the same linear subspace. In majority of existing works on subspace clustering, samples are simply regarded as being independent and identically distributed, that is, arbitrarily ordering samples when necessary. However, this setting ignores sample correlations in their original spatial structure. To address this issue, we propose a tensor low-rank representation (TLRR) for subspace clustering by keeping available spatial information of data. TLRR seeks a lowest-rank representation over all the candidates while maintaining the inherent spatial structures among samples, and the affinity matrix used for spectral clustering is built from the combination of similarities along all data spatial directions. TLRR better captures the global structures of data and provides a robust subspace segmentation from corrupted data. Experimental results on both synthetic and real-world datasets show that TLRR outperforms several established state-of-the-art methods.