Low Rank Global Geometric Consistency for Partial-Duplicate Image Search

Abstract

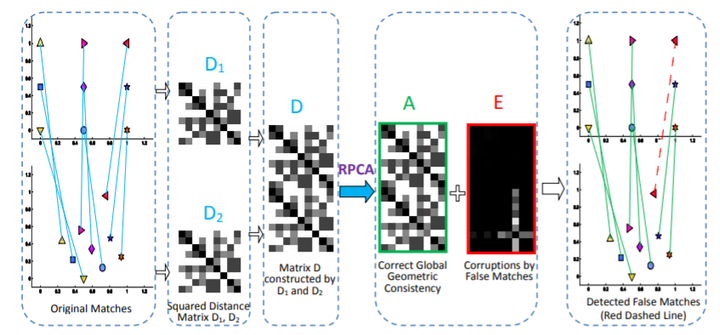
All existing feature point based partial-duplicate image retrieval systems are confronted with the false feature point matching problem. To resolve this issue, geometric contexts are widely used to verify the geometric consistency in order to remove false matches. However, most of the existing methods focus on local geometric contexts rather than global. Seeking global contexts has attracted a lot of attention in recent years. This paper introduces a novel global geometric consistency, based on the low rankness of squared distance matrices of feature points, to detect false matches. We cast the problem of detecting false matches as a problem of decomposing a squared distance matrix into a low rank matrix, which models the global geometric consistency, and a sparse matrix, which models the mismatched feature points. So we arrive at a model of Robust Principal Component Analysis. Our Low Rank Global Geometric Consistency (LRGGC) is simple yet effective and heoretically sound. Extensive experimental results show that our LRGGC is much more accurate than state of the art geometric verification methods in detecting false matches and is robust to all kinds of similarity transformation (scaling, rotation, and translation) and even slight change in 3D views. Its speed is also highly competitive even compared with local geometric consistency based methods.