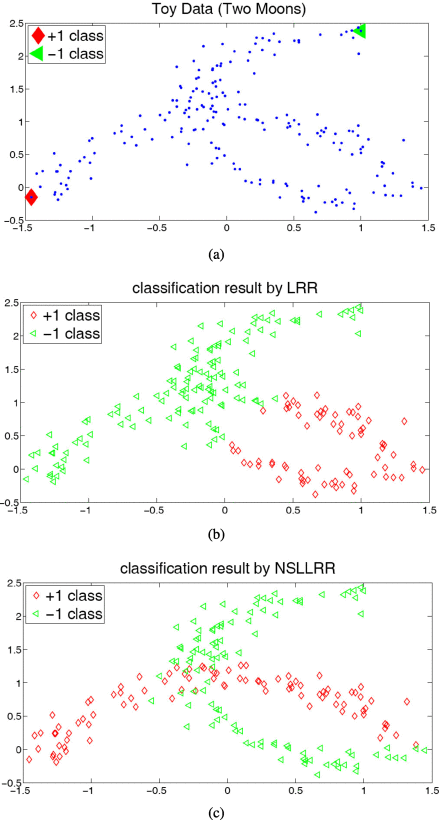
Abstract
Low-rank representation (LRR) has recently attracted a great deal of attention due to its pleasing efficacy in exploring low-dimensional subspace structures embedded in data. For a given set of observed data corrupted with sparse errors, LRR aims at learning a lowest-rank representation of all data jointly. LRR has broad applications in pattern recognition, computer vision and signal processing. In the real world, data often reside on low-dimensional manifolds embedded in a high-dimensional ambient space. However, the LRR method does not take into account the non-linear geometric structures within data, thus the locality and similarity information among data may be missing in the learning process. To improve LRR in this regard, we propose a general Laplacian regularized low-rank representation framework for data representation where a hypergraph Laplacian regularizer can be readily introduced into, i.e., a Non-negative Sparse Hyper-Laplacian regularized LRR model (NSHLRR). By taking advantage of the graph regularizer, our proposed method not only can represent the global low-dimensional structures, but also capture the intrinsic non-linear geometric information in data. The extensive experimental results on image clustering, semi-supervised image classification and dimensionality reduction tasks demonstrate the effectiveness of the proposed method.