Fast Multidimensional Ellipsoid-Specific Fitting by Alternating Direction Method of Multipliers

Abstract

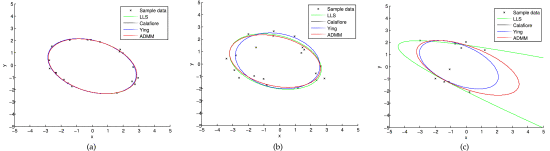
Many problems in computer vision can be formulated as multidimensional ellipsoid-specific fitting, which is to minimize the residual error such that the underlying quadratic surface is a multidimensional ellipsoid. In this paper, we present a fast and robust algorithm for solving ellipsoid-specific fitting directly. Our method is based on the alternating direction method of multipliers, which does not introduce extra positive semi-definiteness constraints. The computation complexity is thus significantly lower than those of semi-definite programming (SDP) based methods. More specifically, to fit $n$ data points into a $p$ dimensional ellipsoid, our complexity is $O(p^6 + np^4)+O(p^3)$ , where the former $O$ results from preprocessing data once , while that of the state-of-the-art SDP method is $O(p^6 + np^4 + n^{rac{3}{2}}p^2)$ for each iteration . The storage complexity of our algorithm is about $rac{1}{2}np^2$ , which is at most $1/4$ of those of SDP methods. Extensive experiments testify to the great speed and accuracy advantages of our method over the state-of-the-art approaches. The implementation of our method is also much simpler than SDP based methods.