Abstract
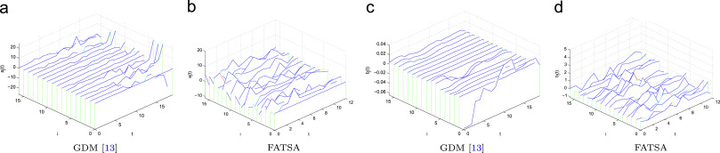
Learning-based partial differential equations (PDEs), which combine fundamental differential invariants into a nonlinear regressor, have been successfully applied to several computer vision and image processing problems. However, the gradient descent method (GDM) for solving the linear combination coefficients among differential invariants is time-consuming. Moreover, when the regularization or constraints on the coefficients become more complex, it is troublesome or even impossible to deduce the gradients. In this paper, we propose a new algorithm, called fast alternating time-splitting approach (FATSA), to solve the linear combination coefficients. By minimizing the difference between the expected output and the actual output of PDEs at each time step, FATSA can solve the linear combination coefficients much faster than GDM. More complex regularization or constraints can also be easily incorporated. Extensive experiments demonstrate that our proposed FATSA outperform GDM in both speed and quality.