Differentiable Linearized ADMM

Abstract

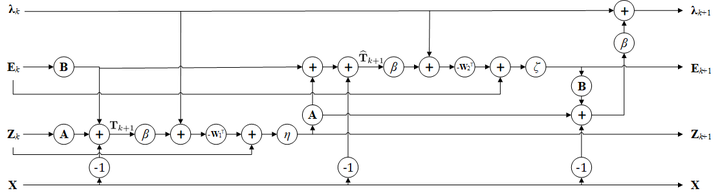
Recently, a number of learning-based optimization methods that combine data-driven architectures with the classical optimization algorithms have been proposed and explored, showing superior empirical performance in solving various illposed inverse problems, but there is still a scarcity of rigorous analysis about the convergence behaviors of learning-based optimization. In particular, most existing analyses are specific to unconstrained problems but cannot apply to the more general cases where some variables of interest are subject to certain constraints. In this paper, we propose Differentiable Linearized ADMM (DLADMM) for solving the problems with linear constraints. Specifically, D-LADMM is a K-layer LADMM inspired deep neural network, which is obtained by firstly introducing some learnable weights in the classical Linearized ADMM algorithm and then generalizing the proximal operator to some learnable activation function. Notably, we rigorously prove that there exist a set of learnable parameters for D-LADMM to generate globally converged solutions, and we show that those desired parameters can be attained by training D-LADMM in a proper way. To the best of our knowledge, we are the first to provide the convergence analysis for the learning-based optimization method on constrained problems..