Maximum-and-Concatenation Networks

Abstract

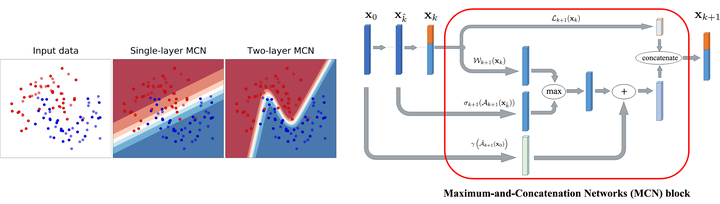
While successful in many fields, deep neural networks (DNNs) still suffer from some open problems such as bad local minima and unsatisfactory generalization performance. Despite the progresses achieved during the past several years, those difficulties have not been overcome completely and are still preventing DNNs from being more successful. In this work, we propose a novel architecture called Maximum-and-Concatenation Networks (MCN) to try eliminating bad local minima and improving generalization ability as well. MCN is a multi-layer network concatenated by a linear part and the maximum of two piecewise smooth functions, and it can approximate a wide range of functions used in practice. Remarkably, we prove that MCN has a very nice property; that is, every local minimum of an $(l+1)$-layer MCN can be better than, at least as good as, the global minima of the network consisting of its first $l$ layers. In other words, via increasing the network depth, MCN can autonomously improve the goodness of its local minima. What is more, it is easy to plug MCN into an existing deep model to make it also have this property. Finally, under mild conditions, we show that MCN can approximate certain continuous function arbitrarily well with high efficiency; that is, the covering number of MCN is much smaller than most existing DNNs such as deep ReLU. Based on this, we further provide a tight generalization bound to guarantee the inference ability of MCN when dealing with testing samples. Experiments on the CIFAR datasets confirm the effectiveness of MCN.