Tree Structure Based Analyses on Compressive Sensing for Binary Sparse Sources

Abstract

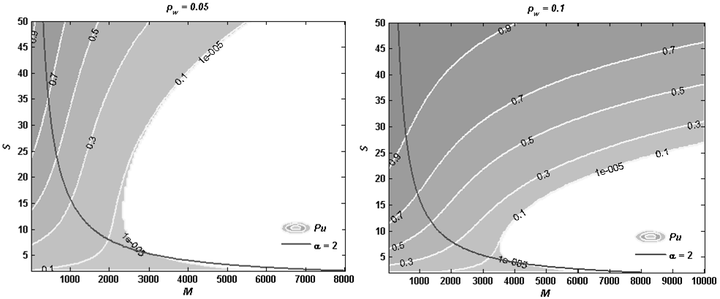
This paper proposes a new approach to theoretically analyze compressive sensing directly from the randomly sampling matrix phi instead of a certain recovery algorithm. For simplifying our analyses, we assume both input source and random sampling matrix as binary. Taking anyone of source bits, we can constitute a tree by parsing the randomly sampling matrix, where the selected source bit as the root. In the rest of tree, measurement nodes and source nodes are connected alternatively according to phi. With the tree, we can formulate the probability if one source bit can be recovered from randomly sampling measurements. The further analyses upon the tree structure reveal the relation between the un-recovery probability with random measurements and the un-recovery probability with source sparsity. The conditions of successful recovery are proven on the parameter S-M plane. Then the results of the tree structure based analyses are compared with the actual recovery process.