Designing Partial Differential Equations for Image Processing by Combining Differential Invariants

Abstract

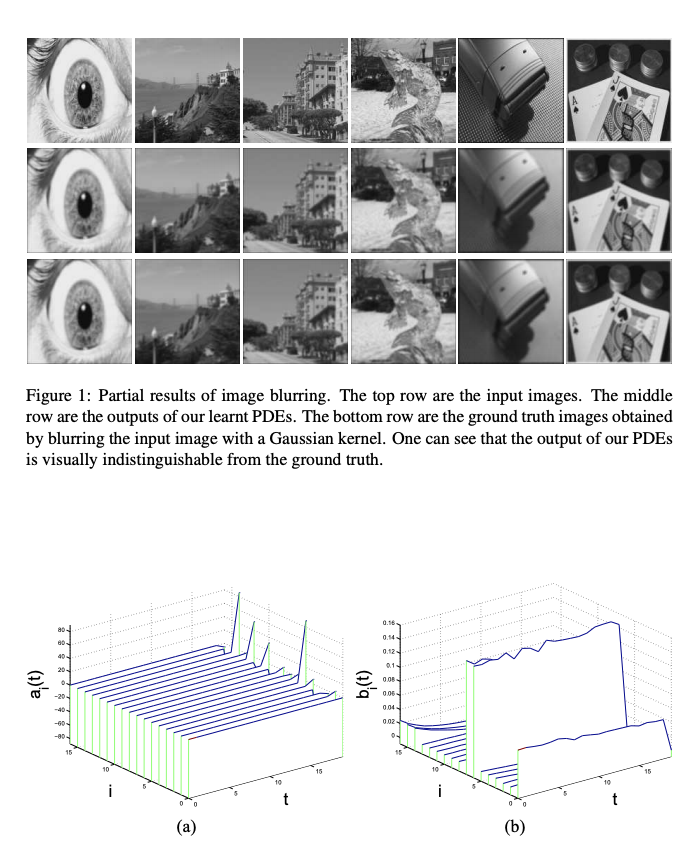
Partial differential equations (PDEs) have been successful for solving many problems in image processing and computer vision. However, designing PDEs usually requires high mathematical skills and good insight to the problems. In this paper, we propose a framework for learning a system of PDEs from real data. Compared to the traditional approaches to designing PDEs, our framework requires much less human intelligence. We assume that the system consists of two PDEs. One controls the evolution of the output and the other is for an indicator function that helps collect global information. As the PDEs should be shift and rotationally invariant, they must be functions of differential invariants that are shift and rotationally invariant. Currently, we assume that the PDEs are simply linear combinations of the fundamental differential invariants up to second order. The combination coefficients can be learnt from real data via an optimal control technique. The exemplary experiments show that the PDEs, designed in our unified way, can solve some image processing problems reasonably well. Hence our framework is very promising. We expect that with future improvements our framework could work for more image processing/computer vision problems.