Determining Step Sizes in Geometric Optimization Algorithms

Abstract

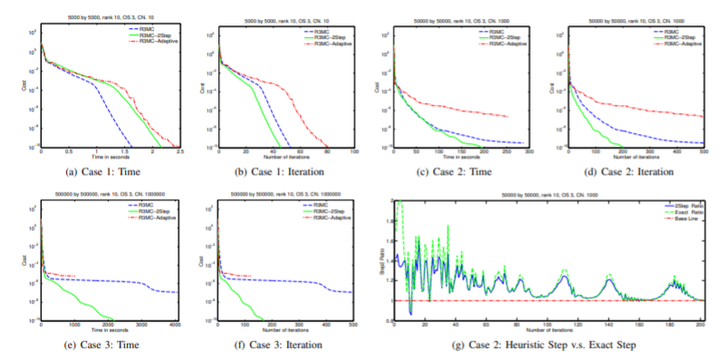
Optimization on Riemannian manifolds is an intuitive generalization of the traditional optimization algorithms in Euclidean spaces. In these algorithms, minimizing along a search direction becomes minimizing along a search curve lying on a manifold. Computing such a curve to be subsequently searched upon is itself computational intensive. We propose a new minimization scheme aiming to find a better step size utilizing the first order information of the search curve. We prove that this scheme can provide further reduction for the cost function when the retraction and the vector transport are collinear. Then we adapt this scheme to propose a heuristic strategy for line search. In numerical experiments, we apply this heuristic strategy to one of the geometric algorithms for matrix completion and show its feasibility and the potential in accelerating computation.