Abstract
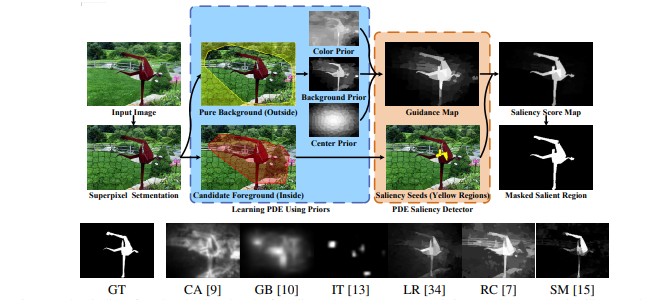
Partial Differential Equations (PDEs) have been successful in solving many low-level vision tasks. However, it is a challenging task to directly utilize PDEs for visual saliency detection due to the difficulty in incorporating human perception and high-level priors to a PDE system. Instead of designing PDEs with fixed formulation and boundary condition, this paper proposes a novel framework for adaptively learning a PDE system from an image for visual saliency detection. We assume that the saliency of image elements can be carried out from the relevances to the saliency seeds (i.e., the most representative salient elements). In this view, a general Linear Elliptic System with Dirichlet boundary (LESD) is introduced to model the diffusion from seeds to other relevant points. For a given image, we first learn a guidance map to fuse human prior knowledge to the diffusion system. Then by optimizing a discrete submodular function constrained with this LESD and a uniform matroid, the saliency seeds (i.e., boundary conditions) can be learnt for this image, thus achieving an optimal PDE system to model the evolution of visual saliency. Experimental results on various challenging image sets show the superiority of our proposed learning-based PDEs for visual saliency detection.