Limits of Learning-Based Superresolution Algorithms

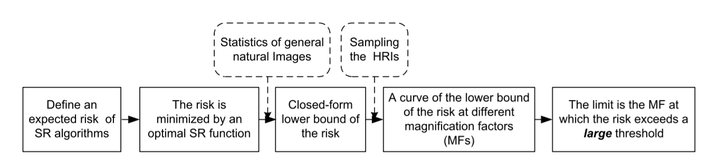
Abstract

Learning-based superresolution (SR) is a popular SR technique that uses application dependent priors to infer the missing details in low resolution images (LRIs). However, their erformance still deteriorates quickly when the magnification factor is only moderately large. This leads us to an important problem: “Do limits of learning-based SR algorithms exist?” This paper is the first attempt to shed some light on this problem when the SR algorithms are designed for general natural images. We first define an expected risk for the SR algorithms that is based on the root mean squared error between the superresolved images and the ground truth images. Then utilizing the statistics of general natural images, we derive a closed form estimate of the lower bound of the expected risk. The lower bound only involves the covariance matrix and the mean vector of the high resolution images (HRIs) and hence can be computed by sampling real images. We also investigate the sufficient number of samples to guarantee an accurate estimate of the lower bound. By computing the curve of the lower bound w.r.t. the magnification factor, we could estimate the limits of learning-based SR algorithms, at which the lower bound of the expected risk exceeds a relatively large threshold. We perform experiments to validate our theory. And based on our observations we conjecture that the limits may be independent of the size of either the LRIs or the HRIs.