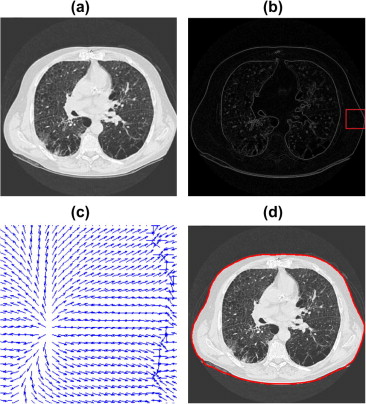
Abstract
Gradient vector flow (GVF) and generalized GVF (GGVF) have been widely applied in many image processing applications. The high cost of GVF/GGVF computation, however, has restricted their potential applications on images with large size. Motivated by progress in fast image restoration algorithms, we reformulate the GVF/GGVF computation problem using the convex optimization model with equality constraint, and solve it using the inexact augmented Lagrangian method (IALM). With fast Fourier transform (FFT), we provide two novel simple and efficient algorithms for GVF/GGVF computation, respectively. To further improve the computational efficiency, the multiresolution approach is adopted to perform the GVF/GGVF computation in a coarse-to-fine manner. Experimental results show that the proposed methods can improve the computational speed of the original GVF/GGVF by one or two order of magnitude, and are more efficient than the state-of-the-art methods for GVF/GGVF computation.