Abstract
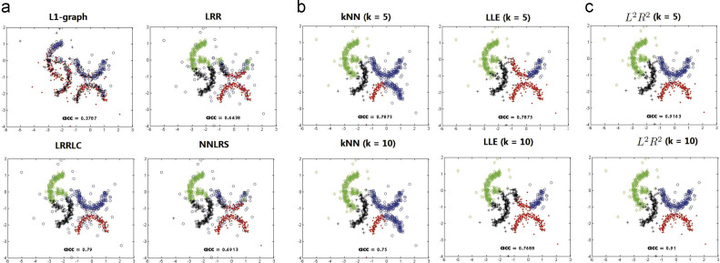
Building a good graph to represent data structure is important in many computer vision and machine learning tasks such as recognition and clustering. This paper proposes a novel method to learn an undirected graph from a mixture of nonlinear manifolds via Locality-Preserving Low-Rank Representation (), which extents the original LRR model from linear subspaces to nonlinear manifolds. By enforcing a locality-preserving sparsity constraint to the LRR model, guarantees its linear representation to be nonzero only in a local neighborhood of the data point, and thus preserves the intrinsic geometric structure of the manifolds. Its numerical solution results in a constrained convex optimization problem with linear constraints. We further apply a linearized alternating direction method to solve the problem. We have conducted extensive experiments to benchmark its performance against six state-of-the-art algorithms. Using nonlinear manifold clustering and semi-supervised classification on images as examples, the proposed method significantly outperforms the existing methods, and is also robust to moderate data noise and outliers.