Abstract
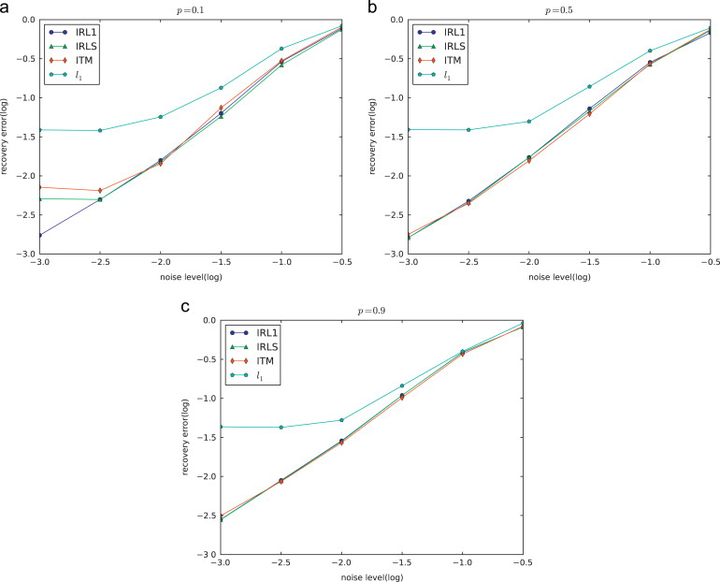
Recently, compressed sensing has been widely applied to various areas such as signal processing, machine learning, and pattern recognition. To find the sparse representation of a vector w.r.t. adictionary, anℓ1minimization problem, which is convex, is usually solved in order to overcome thecomputational difficulty. However, to guarantee that theℓ1minimizer is close to the sparsest solution,strong incoherence conditions should be imposed. In comparison, nonconvex minimization problemssuch as those with theℓpð0opo1Þpenalties require much weaker incoherence conditions and smallersignal to noise ratio to guarantee a successful recovery. Hence theℓpð0opo1Þregularization serves as abetter alternative to the popularℓ1one. In this paper, we review some typical algorithms,Iteratively Reweighted ℓ1 minimization(IRL1),Iteratively Reweighted Least Squares(IRLS) (and its general form General Iteratively Reweighted Least Squares(GIRLS)), and Iteratively Thresholding Method(ITM), forℓp minimization and do comprehensive comparison among them, in which IRLS is identified as having the bestperformance and being the fastest as well.