Factorization for Projective and Metric Reconstruction via Truncated Nuclear Norm

Abstract

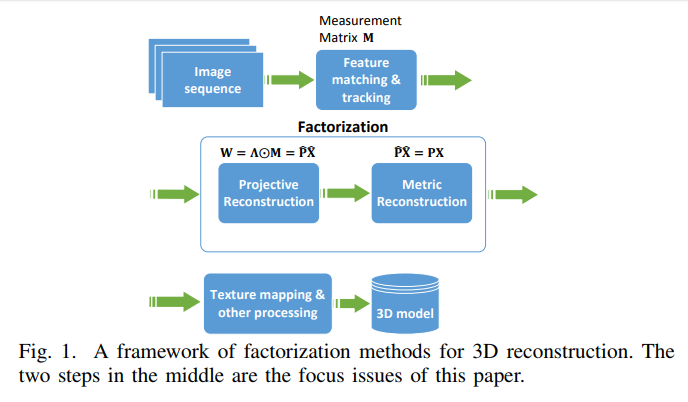
Structure from motion (SfM) is a crucial and widely studied problem in computer vision. Recently, the factorization framework for SfM was formulated as a low rank approximation problem: the rank of rescaled measurement matrix is always smaller than four. Since the rank function is non-convex, a common practice is to replace with its convex surrogate, i.e., the nuclear norm. However, nuclear norm sometimes gets unsatisfactory results. In this paper, we apply the recently proposed truncated nuclear norm to handle the factorization framework in a non-convex way, which heavily penalizes the singular values beyond the desired rank. We further introduce weighted `1-norm to handle missing data and outliers uniformly. Based on truncated nuclear norm, we propose two factorization models for projective reconstruction and metric reconstruction, respectively. We also proposed an extremely efficient algorithm to tackle one of the optimization sub-problems. Extensive experiments on synthetic and real datasets verify the effectiveness of our method for projective and metric reconstructions. Our method achieves higher accuracy in 3D reconstruction and is more robust to missing data and outliers.