Low-Dimension-to-High-Dimension Generalization And Its Implications for Length Generalization

Abstract

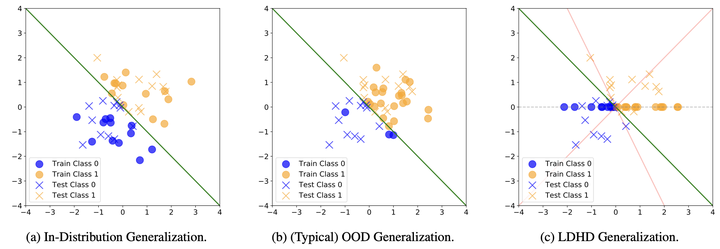
Low-Dimension-to-High-Dimension (LDHD) generalization, a subset of Out-of-Distribution (OOD) generalization, involves training on a low-dimensional subspace and testing in a high-dimensional space. Assuming instances are generated from latent variables reflecting problem scale, LDHD generalization captures the inherent scaling challenge of length gener- alization. We theoretically show that LDHD generalization is unattainable without appropriate inductive bias. Focusing on Boolean functions, we demonstrate that different architectures trained with (S)GD converge to min-degree interpolators w.r.t. different linearly independent sets, achieving LDHD generalization only when the target function aligns with this bias. From the perspective of LDHD generalization for length generalization, we explain the success of CoT in restructuring latent space for improved LDHD generalization. We further propose a principle for designing position embeddings to address both LDHD generalization and data format nuisances separately. Following the principle, we introduce RPE-Square, a novel embedding that enhances RPE to better handle data formats.